Notes 5

Sie können diese Seite ausdrucken oder mit einem PDF-Drucker in ein PDF umwandeln, um Ihre eigenen Notizen hinzuzufügen.

Willkommen!

In den vorangegangenen Wochen haben Sie die grundlegenden Bausteine der Programmierung kennengelernt.
Alles, was Sie in C gelernt haben, wird Sie in die Lage versetzen, diese Bausteine in höheren Programmiersprachen wie Python umzusetzen.
Heute werden wir über die Organisation von Daten im Speicher und über Designmöglichkeiten sprechen, die sich aus Ihrem wachsenden Wissen ergeben.

Daten-Strukturen

Datenstrukturen sind im Wesentlichen Organisationsformen im Speicher.
Es gibt viele Möglichkeiten, Daten im Speicher zu organisieren.
Abstrakte Datenstrukturen sind diejenigen, die wir uns konzeptionell vorstellen können. Wenn man etwas über Informatik lernt, ist es oft nützlich, mit diesen konzeptionellen Datenstrukturen zu beginnen. Wenn man sie lernt, fällt es einem später leichter zu verstehen, wie man konkretere Datenstrukturen implementiert.

Stacks und Queues

Queues (gängige Aussprache i.d.R. “kjuus”, auf Deutsch: Warteschlagen) gehören zu den sog. Abstrakten Datentypen. Diese zeichnen sich dadurch aus, dass sie bestimmte Eigenschaften und Operationen haben, aber intern auf unterschiedliche Art und Weise implementiert werden können. Im Idealfall spielt die Art und Weise der Implementation für die Benutzung keine Rolle (Prinzip der Kapselung).
Queues haben spezifische Eigenschaften. Sie behandeln Daten gemäß des Prinzips FIFO, d.h. “first in first out”. Stellen Sie sich vor, Sie stehen in einer Schlange für eine Fahrt in einem Vergnügungspark. Die erste Person in der Schlange darf zuerst fahren. Die letzte Person in der Schlange darf als letzte fahren.
Queues sind mit bestimmten Aktionen verbunden. Zum Beispiel kann ein Gegenstand in die Warteschlange gestellt werden, d. h. der Gegenstand kann sich in die Schlange einreihen (engl. enqueue). Außerdem kann ein Gegenstand dequeued werden, also die Warteschlange verlassen, wenn er den Anfang der Schlange erreicht und bearbeitet wird.

Im Code könnte man eine Queue wie folgt realisieren:

typedef struct
{
    person people[CAPACITY];
    int size;
}
queue;

Die Implementation der beiden Operationen von Queues schauen wir uns in unserem Kurs nicht an; sie sind aber nicht schwer.
Das Gegenstück zu Queues sind Stacks (auf Deutsch: Stapel). Die Eigenschaften eines Stacks unterscheiden sich grundlegend von denen einer Queue. Genauer gesagt arbeitet ein Stack gemäß des Prinzips LIFO, d.h. “last in first out”. Genau wie beim Stapeln von Tabletts in einer Cafeteria muss ein Tablett, das als letztes auf einen Stapel gestellt wird, als erstes heruntergenommen werden.
Auch Stacks haben bestimmte Aktionen, die mit ihnen verbunden sind. Zum Beispiel legt die Aktion push etwas auf einen Stack. Und mit der Aktion pop wird etwas vom oberen Ende des Stapels entfernt.
Im Code kann man einen Stack wie folgt implementieren:
```
typedef struct
{
    person people[CAPACITY];
    int size;
}
stack;
```
Beachten Sie, dass das Array namens people vom Typ person ist. Die CAPACITY gibt an, wie viele Elemente maximal im Stapel Platz finden. Die Ganzzahl size gibt an, wie voll der Stapel tatsächlich ist, unabhängig davon, wie viel er fassen könnte.
Ist Ihnen aufgefallen, dass Stack und Queue eine struct mit den gleichen Feldern nutzen? Das ist kein Fehler; beide Datentypen sind sich sehr ähnlich. Das unterschiedliche Verhalten wird durch die Implementation der Operationen erreicht.
Schauen Sie sich die Varianten der Implementation eines Stacks als Array oder als Verkettete Liste im Short-Video zu Stacks an.
Sie können sich vorstellen, dass der obige Code eine Einschränkung hat. Denn die Kapazität des Arrays ist in diesem Code immer vorgegeben. Es kann daher vorkommen, dass der Stapel vorsorglich überdimensioniert angelegt wird. Wenn dann nur einer von 5000 Plätzen im Stapel verwendet wird, ist das nicht besonders effizient.
Es wäre schön, wenn unser Stapel dynamisch wäre - er soll also wachsen können, wenn Elemente hinzugefügt werden.

Größenänderung von Arrays

In Woche 2 haben wir Sie mit Ihrer ersten Datenstruktur bekannt gemacht.
Ein Array ist ein Block aus zusammenhängendem Speicher.
Sie können sich ein Array wie folgt vorstellen:

array
Im Speicher befinden sich weitere Werte, die von anderen Programmen, Funktionen und Variablen gespeichert werden. Bei vielen dieser Werte kann es sich um ungenutzte Garbage-Values handeln, die zu einem bestimmten Zeitpunkt verwendet wurden, jetzt aber zur Verwendung zur Verfügung stehen.

array inside memory
Stellen Sie sich vor, Sie wollten einen vierten Wert 4 in unserem Array speichern? In diesem Fall müssten wir einen neuen Speicherbereich zuweisen und das alte Array in den neuen Bereich verschieben. Dieser neue Speicherbereich wäre zunächst mit Garbage-Values gefüllt.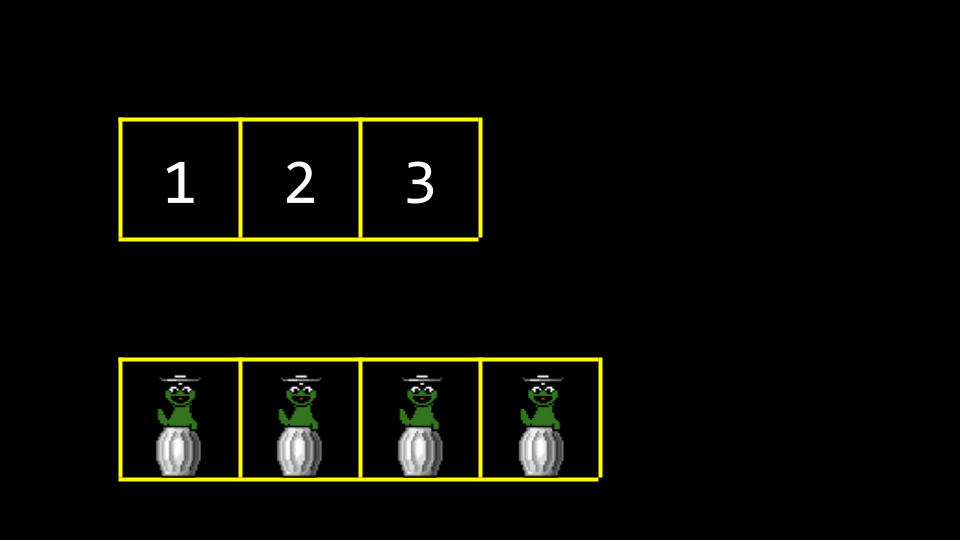

zwei Arrays mit Müllwerten
Wenn unsere Werte dann zum neuen Speicherbereich hinzugefügt werden, werden die alte Garbage-Values überschrieben.

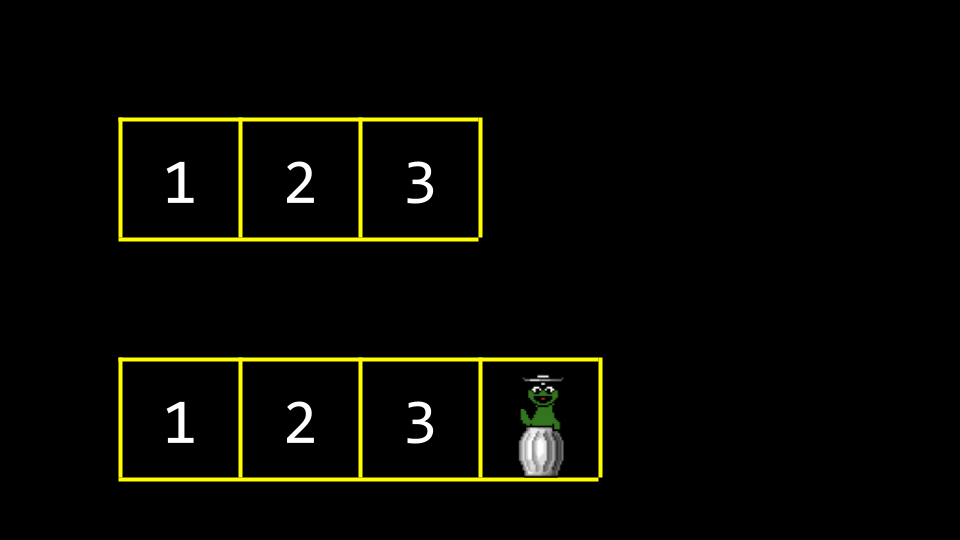
zwei Arrays mit Müllwert
Schließlich würden alle alten Müllwerte mit unseren neuen Daten überschrieben worden sein.

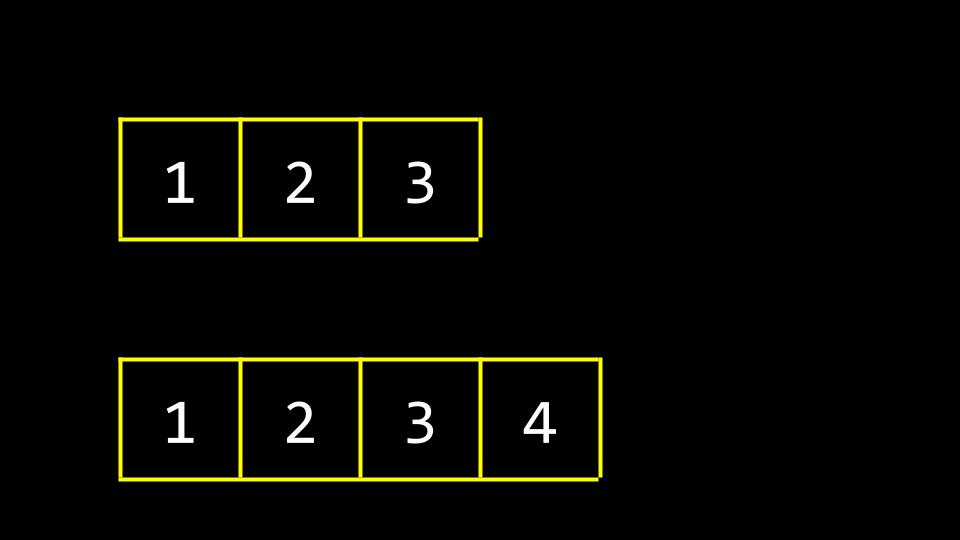
zwei Arrays mit Müllwert
Einer der Nachteile dieses Ansatzes ist, dass er schlecht konzipiert ist: Jedes Mal, wenn wir eine Zahl hinzufügen, müssen wir das alte Array komplett Element für Element kopieren. Das erzeugt Aufwand in der Größenordnung von $O(n)$.
Wäre es nicht schön, wenn wir in der Lage wären, die “4” irgendwo anders im Speicher abzulegen? Per Definition wäre dies kein Array mehr, weil 4 nicht mehr in einem zusammenhängenden Speicher liegen würde.

Geben Sie in Ihrem Terminal code list.c ein und schreiben Sie den folgenden Code:

// Implementiert eine Liste von Zahlen mit einem Array von fester Größe

#include <stdio.h>

int main(void)
{
    int list[3];

    list[0] = 1;
    list[1] = 2;
    list[2] = 3;

    for (int i = 0; i < 3; i++)
    {
        printf("%i\n", list[i]);
    }
}

Beachten Sie, dass die obige Darstellung dem, was wir in diesem Kurs gelernt haben, sehr ähnlich ist. Wir haben Speicher, der für drei Elemente vorbesetzt ist.

Aufbauend auf unserem in letzter Zeit erworbenen Wissen können wir unser Verständnis von Pointern nutzen, um diesen Code besser zu gestalten. Ändern Sie Ihren Code wie folgt:

#include <stdio.h>
#include <stdlib.h>

int main(void)
{
    int *list = malloc(3 * sizeof(int)); // nun dynamisch Speicher allokieren
    if (list == NULL)
    {
        return 1;
    }

    list[0] = 1; // keine Änderung nötig (wir behandeln den List-Pointer wie ein Array)
    list[1] = 2; // Wiederholung Pointer-Arithmetik: list[1] entspricht *(list + 1 * 4)
    list[2] = 3;

    // Nun merken wir, dass wir noch ein viertes Element bräuchten.
    // Also reservieren wir noch einmal Speicher.

    int *tmp = malloc(4 * sizeof(int));
    if (tmp == NULL)
    {
        free(list); // valgrind beschwert sich, wenn wir free vergessen (Speicher wird aber sowieso beim Beenden freigegeben)
        return 1;
    }

    // bisherige Elemente umkopieren
    for (int i = 0; i < 3; i++)
    {
        tmp[i] = list[i];
    }

    tmp[3] = 4;

    // alte Liste freigeben (3 Elemente)
    free(list);

    // list soll nun auf den neuen Speicherbereich zeigen
    list = tmp;

    for (int i = 0; i < 4; i++)
    {
        printf("%i\n", list[i]);
    }

    free(list); // Speicher freigeben
    return 0;
}

Beachten Sie, dass eine Liste mit drei Ganzzahlen erstellt wird. Dann können drei Speicheradressen die Werte 1, 2 und 3 zugewiesen werden. Dann wird eine Liste der Größe 4 erstellt. Anschließend wird die erste Liste in die zweite kopiert. Der Wert für 4 wird der Liste tmp hinzugefügt. Da der Speicherblock, auf den list zeigt, nicht mehr verwendet wird, wird er mit dem Befehl free(list) freigegeben. Schließlich wird der Compiler angewiesen, den Pointer von list jetzt auf den Speicherblock zu zeigen, auf den tmp zeigt. Der Inhalt von list wird ausgedruckt und dann freigegeben.

Es ist nützlich, sich list und tmp als Wegweiser vorzustellen, die auf einen Teil des Speichers zeigen. Wie im obigen Beispiel zeigte list zu einem Zeitpunkt auf ein Array der Größe 3. Am Ende wurde list angewiesen, auf ein Speicherstück der Größe 4 zu zeigen. Technisch gesehen zeigten tmp und list am Ende des obigen Codes beide auf denselben Speicherblock.
Man könnte versucht sein, viel mehr Speicher zuzuweisen, als für die Liste erforderlich ist, z. B. 30 Elemente anstelle der erforderlichen 3 oder 4. Dies ist jedoch schlechtes Design, da es Systemressourcen verbraucht, obwohl diese möglicherweise gar nicht benötigt werden.

Verkettete Listen

In den letzten Wochen haben Sie drei nützliche Primitive kennengelernt. Eine struct ist ein Datentyp, den Sie selbst definieren können. Ein . in Punktschreibweise ermöglicht den Zugriff auf Variablen innerhalb dieser Struktur. Der Operator * wird verwendet, um einen Pointer zu deklarieren oder eine Variable zu derefenzieren.
Heute lernen Sie den ->-Operator kennen, also den Pfeil. Dieser Operator geht zu einer Adresse und sieht innerhalb einer Struktur nach. Eine ausführliche Erklärung finden Sie im Short zu Strukturen.
Eine Verkettete Liste ist eine der mächtigsten Datenstrukturen in C. Eine verkettete Liste erlaubt es Ihnen, Werte zusammenzufassen, die sich in verschiedenen Bereichen des Speichers befinden. Außerdem können Sie die Liste dynamisch vergrößern und verkleinern, wenn Sie es wünschen.
Sie können sich drei Werte vorstellen, die in drei verschiedenen Speicherbereichen gespeichert sind:

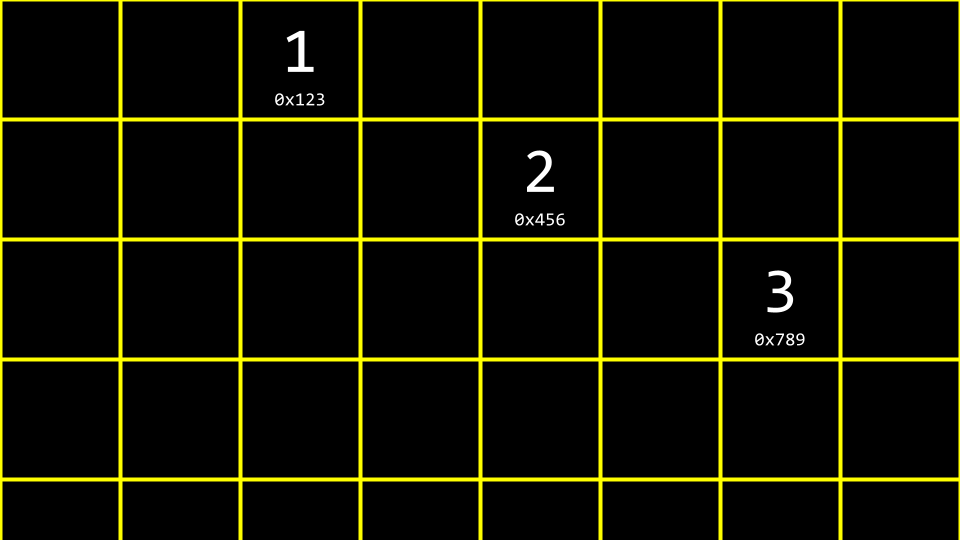
drei Werte im Speicher
Wie könnte man diese Werte in einer Liste zusammenfügen?
Wir könnten uns diese oben abgebildeten Daten wie folgt vorstellen:

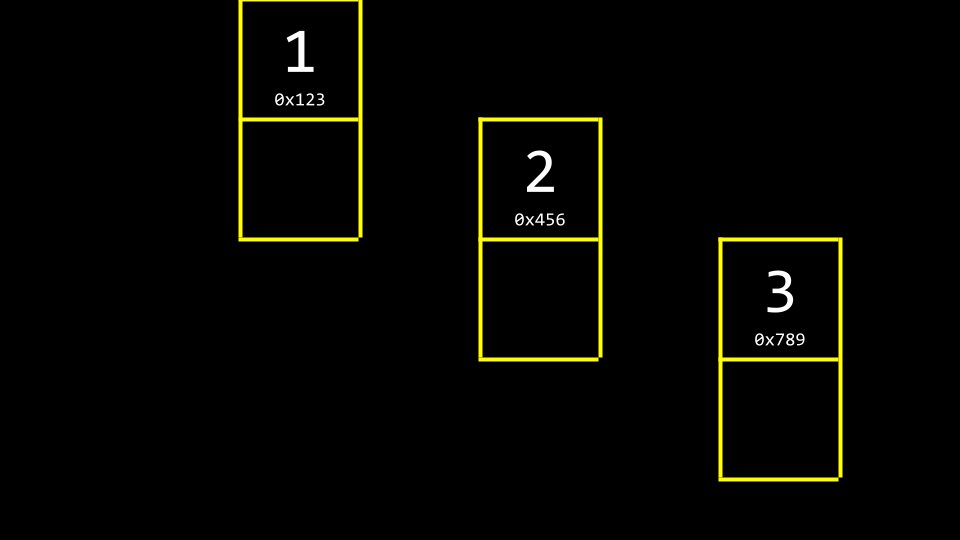
drei Werte im Speicher
Wir könnten mehr Speicherplatz verwenden, um zu wissen, wo sich das nächste Element befindet.

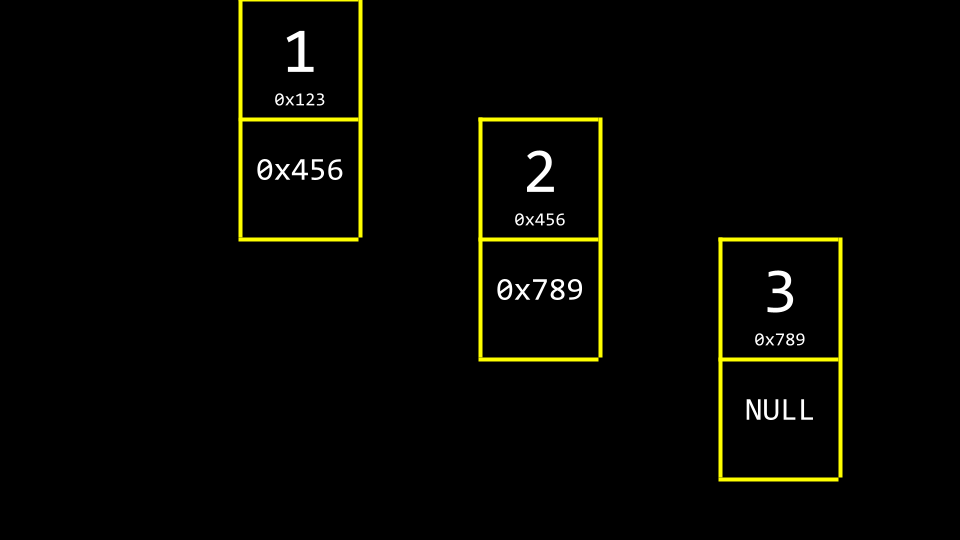
drei Werte im Speicher

Beachten Sie, dass NULL verwendet wird, um anzuzeigen, dass nichts anderes nächstes in der Liste ist.
Typischerweise würde man noch ein weiteres Element im Speicher behalten, einen Pointer, der das erste Element in der Liste verfolgt.

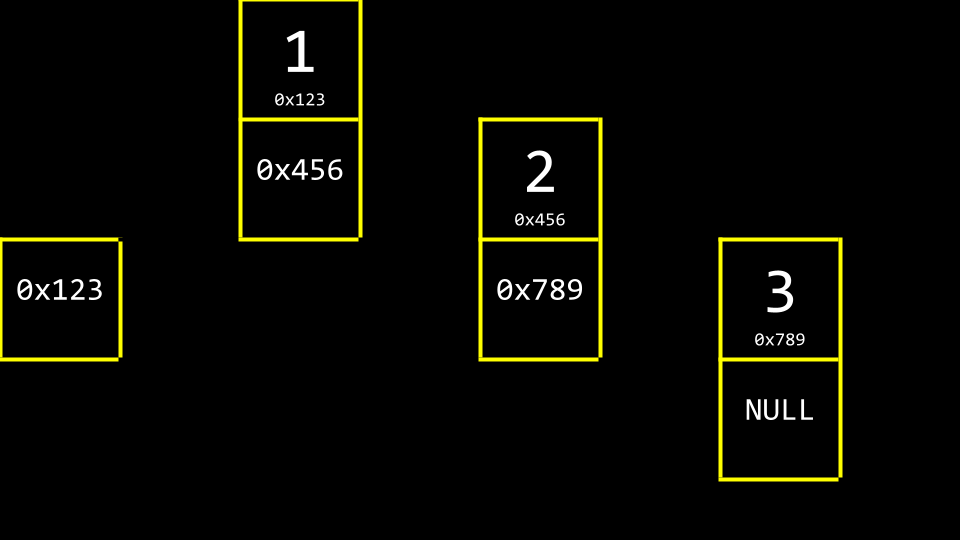
drei Werte im Speicher mit Zeiger
Abstrahiert man von den Speicheradressen, sieht die Liste wie folgt aus:

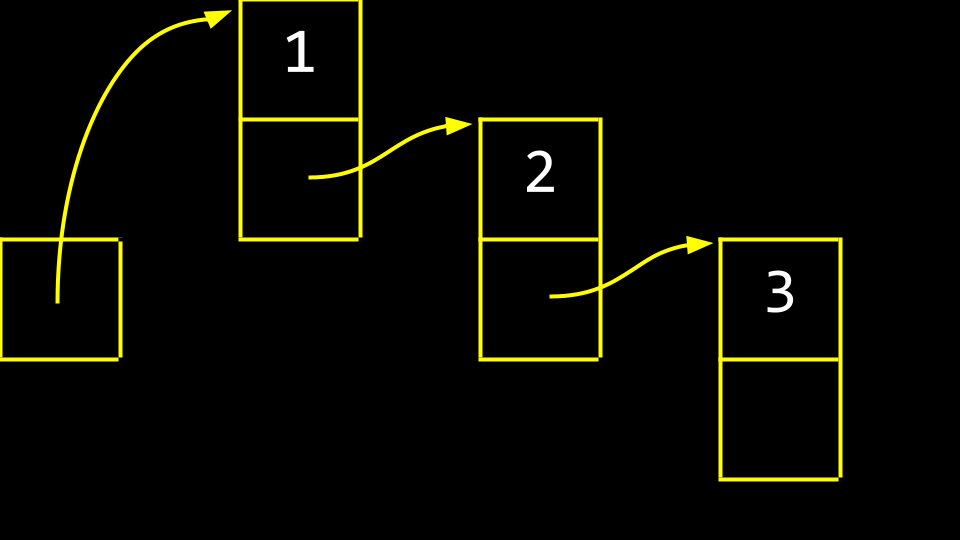
drei Werte im Speicher mit Zeiger
Diese Felder werden Knoten genannt. Ein Knoten enthält sowohl einen Datenelement als auch einen Pointer namens next. Im Code können Sie sich einen Knoten wie folgt vorstellen:
```
typedef struct node
{
    int number;
    struct node *next;
}
node;
```
Beachten Sie, dass das Element in diesem Knoten eine Ganzzahl namens “number” ist. Zweitens ist ein Pointer auf einen Knoten namens “next” enthalten, der auf einen anderen Knoten irgendwo im Speicher verweist.
Wir werden uns den Prozess der Erstellung einer verknüpften Liste erst einmal konzeptionell überlegen. Zunächst wird node *list deklariert. Zunächst enthält der Pointer noch ein Garbage-Value, d.h. er zeigt irgendwo hin.

verknüpfte Liste
Als nächstes wird für einen Knoten namens “n” Speicher allokiert.

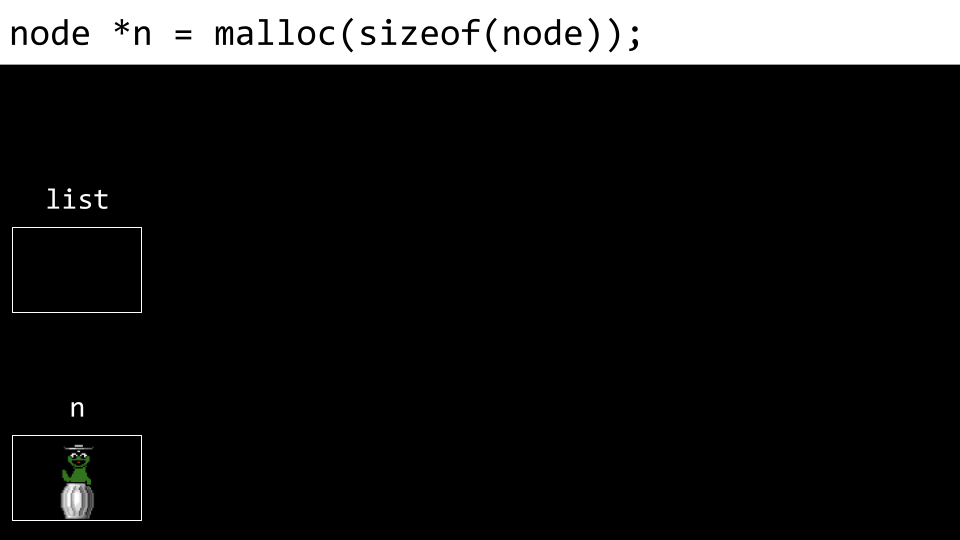
linked list
Als nächstes wird der “number” des Knotens der Wert “1” zugewiesen.

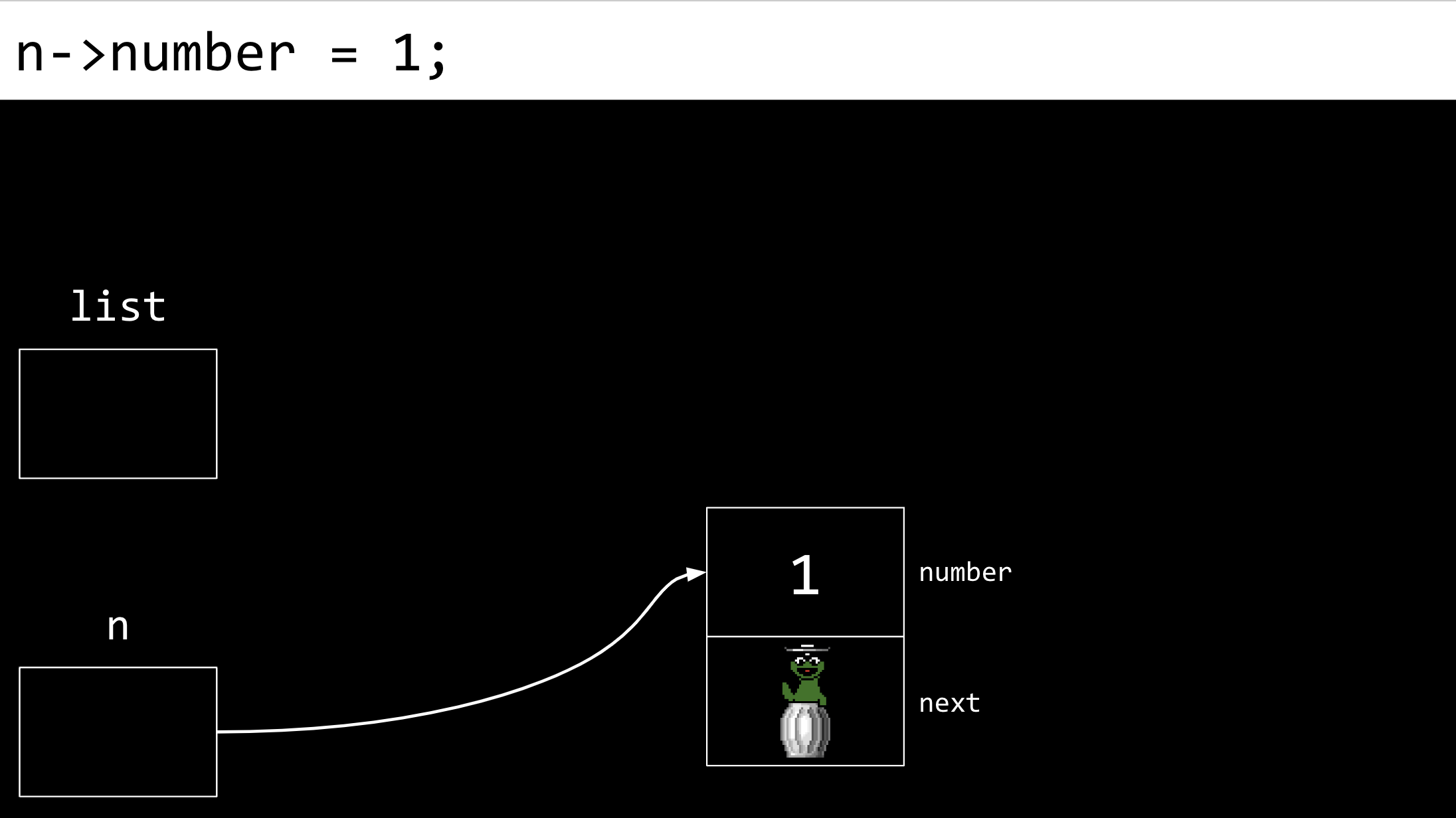
linked list
Als nächstes wird dem Feld “next” des Knotens “NULL” zugewiesen.

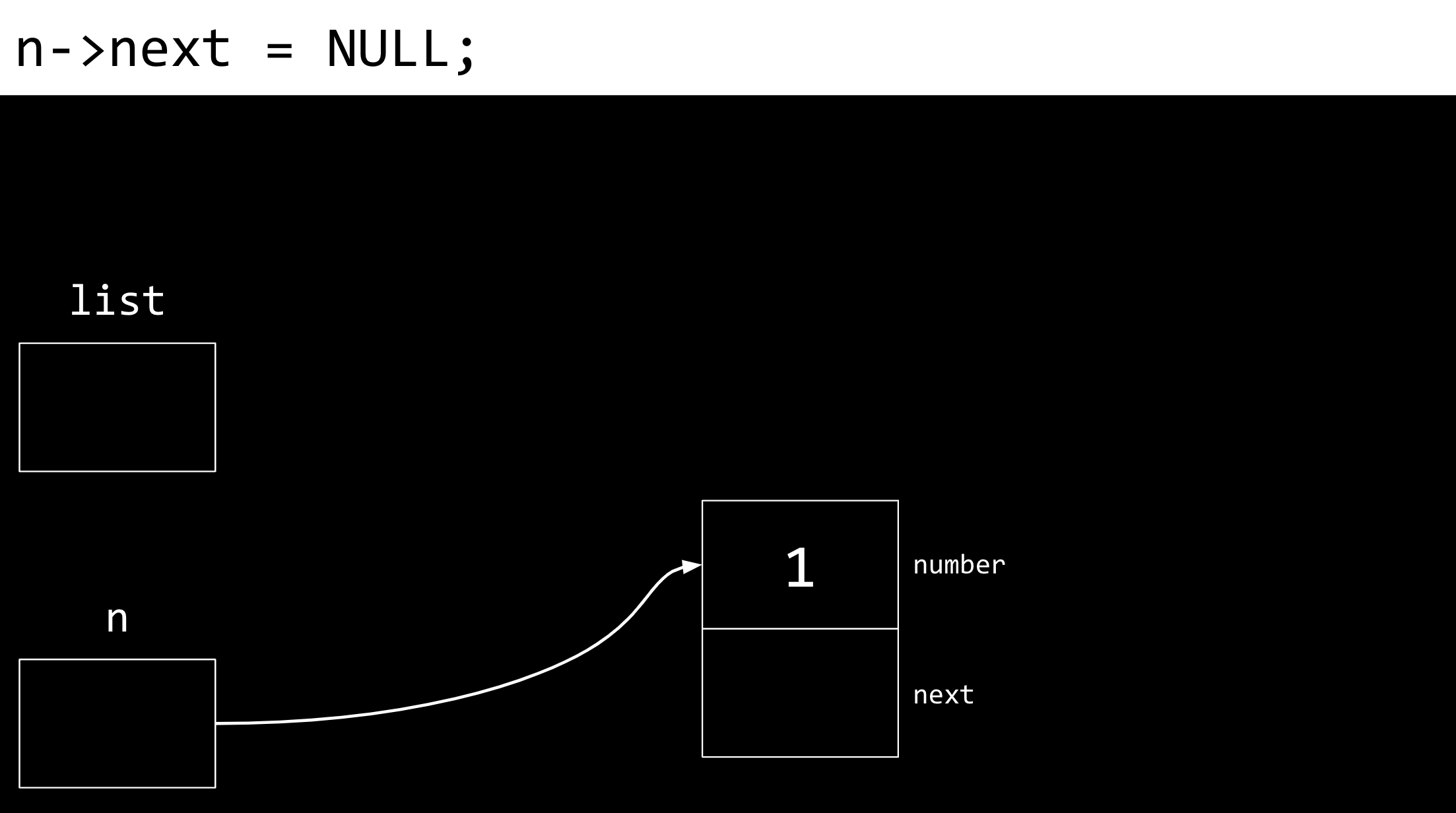
linked list
Als nächstes lassen wir list auf die Speicherstelle zeigen, auf die n zeigt. n und list zeigen nun auf dieselbe Stelle.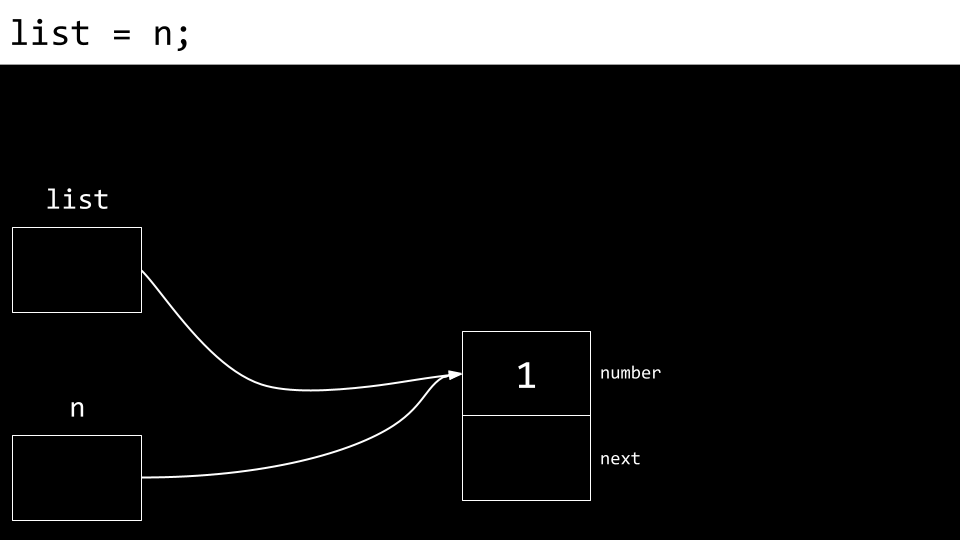

linked list
Dann wird ein neuer Knoten erstellt. Sowohl das Feld “number” als auch das Feld “next” sind zunächst mit Garbage-Werten gefüllt.

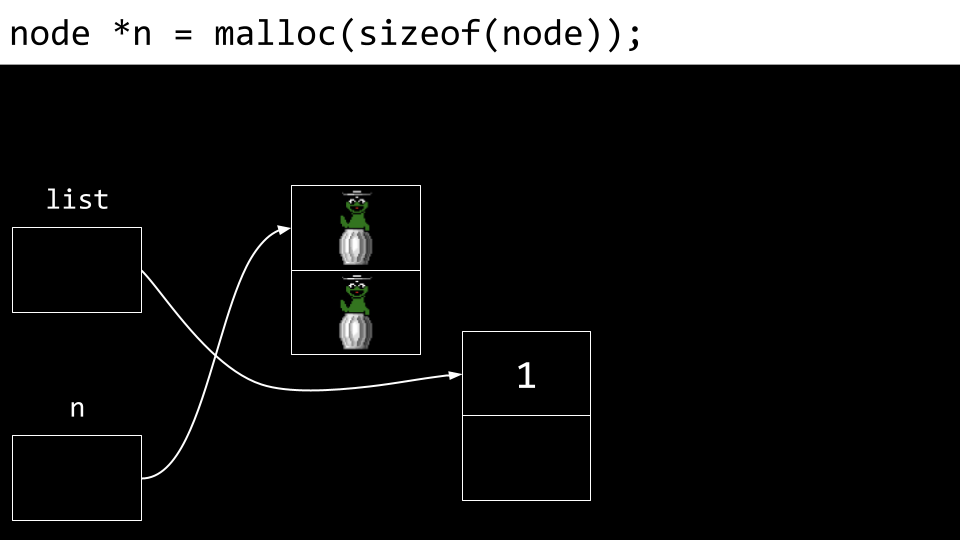
linked list
Der Wert “number” des Knotens “n” (des neuen Knotens) wird auf “2” gesetzt.

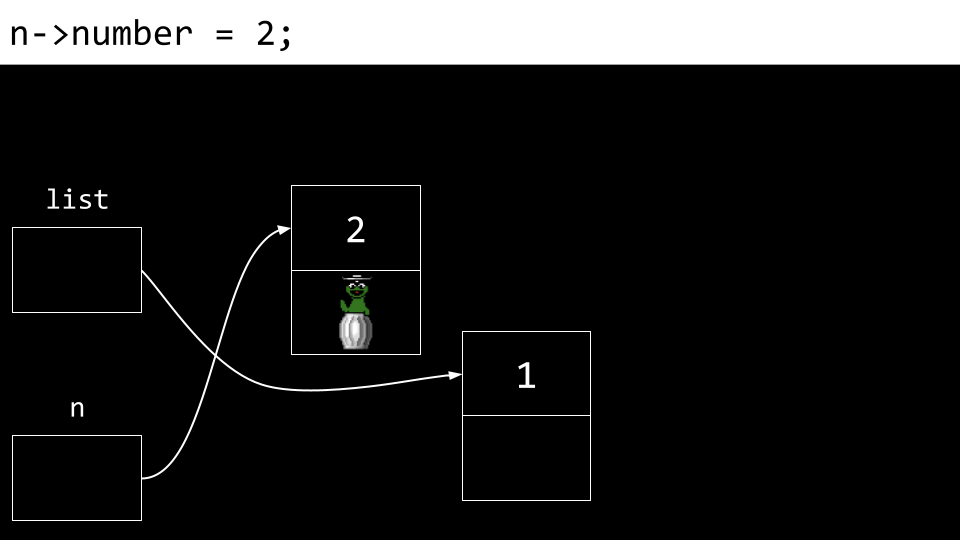
linked list
Außerdem wird auch das Feld “next” aktualisiert.

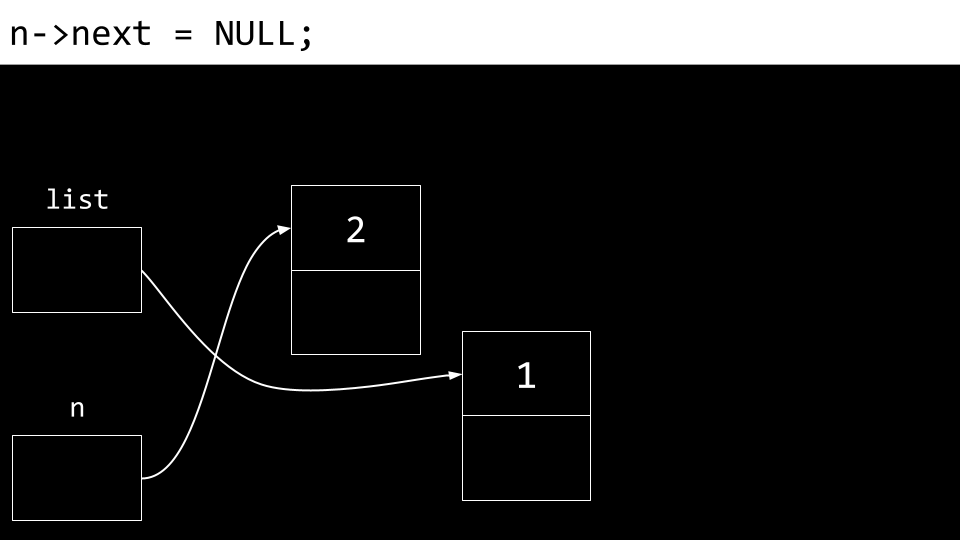
linked list
Am wichtigsten ist, dass wir unsere Verbindung zu keinem dieser Knoten verlieren wollen, damit sie nicht für immer verloren gehen. Dementsprechend lassen wir den “next”-Pointer auf denselben Speicherplatz zeigen wie “list”, also auf den Beginn unserer bereits vorhandenen Liste.

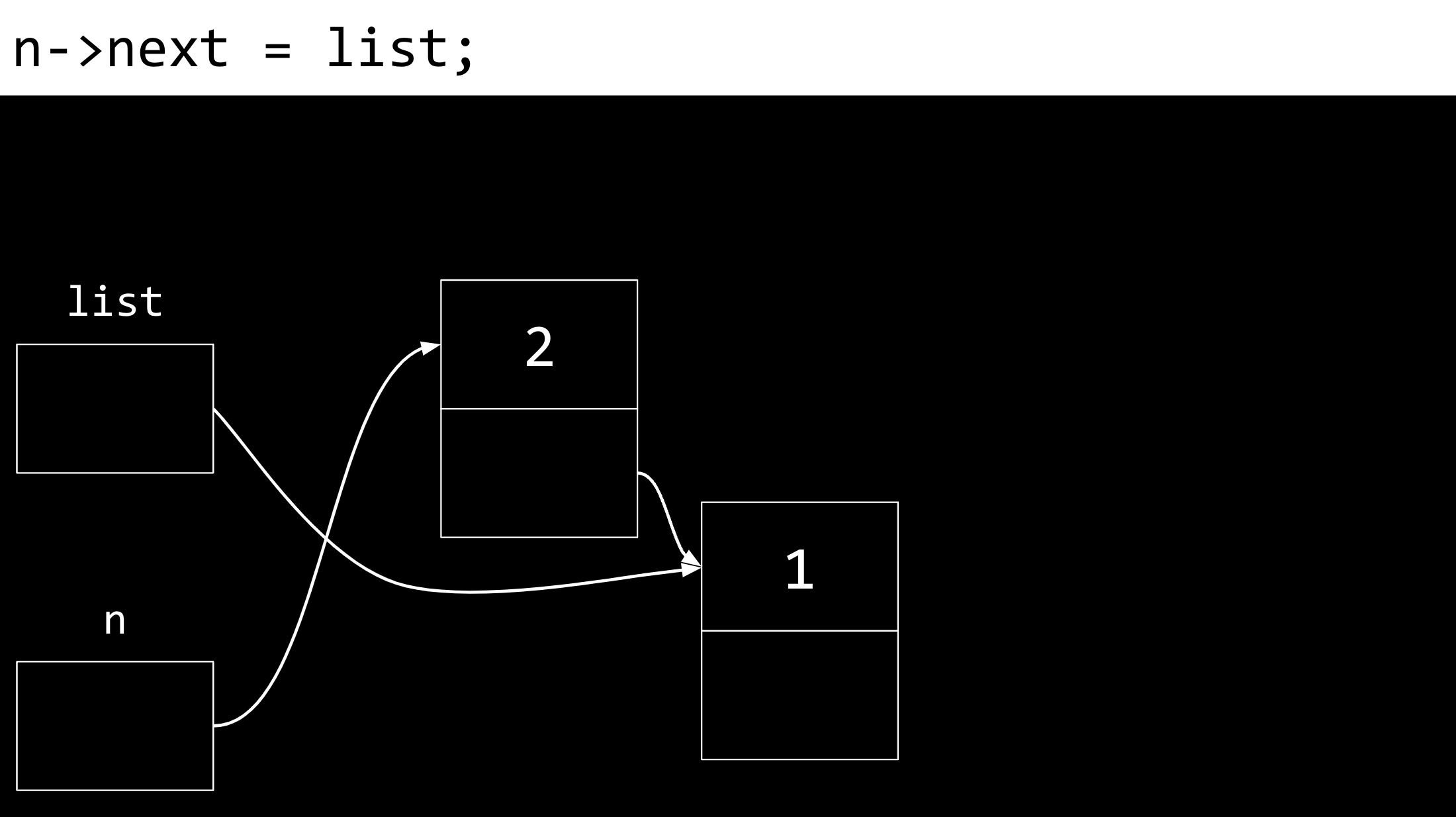
linked list
Schließlich wird “list” aktualisiert. Es zeigt nun auf “n”, also auf den neuen Kopf der Liste. Wir haben nun eine verknüpfte Liste mit zwei Elementen.

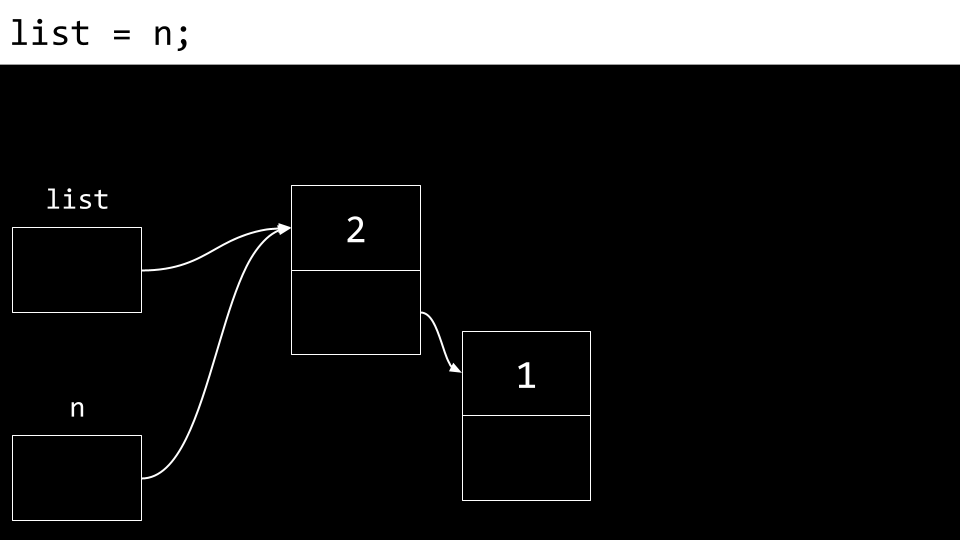
linked list

Um dies in Code umzusetzen, ohne die Schritte mehrfach zu wiederholen, ändern Sie Ihren Code wie folgt:

// Fügt Zahlen in eine verknüpfte Liste ein und verwendet eine while-Schleife zum Ausgeben

#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct node
{
    int number;
    struct node *next;
}
node;

int main(int argc, char *argv[])
{
    node *list = NULL; // guter Stil: immer erst auf NULL setzen

    // Für jedes Befehlszeilenargument
    for (int i = 1; i < argc; i++)
    {
        // Argument in int umwandeln
        int number = atoi(argv[i]);

        // Knoten allokieren
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = number;
        n->next = NULL; // guter Stil, wird aber gleich überschrieben

        // Knoten der Liste voranstellen
        n->next = list;
        list = n;
    }

    // Liste ausgeben (Überlegen Sie: in welcher Reihenfolge?)
    node *ptr = list;
    while (ptr != NULL)
    {
        printf("%i\n", ptr->number);
        ptr = ptr->next;
    }

    // Speicher freigeben
    ptr = list;
    while (ptr != NULL)
    {
        node *next = ptr->next;
        free(ptr);
        ptr = next;
    }
}

Beachten Sie, dass das, was der Benutzer in der Befehlszeile eingibt, in das Feld number eines Knotens namens n eingetragen wird, und dann wird dieser Knoten zu list hinzugefügt. Zum Beispiel setzt ./list 1 2 die Zahl 1 in das Feld number eines Knotens namens n, setzt dann einen Zeiger auf list in das Feld next des Knotens und aktualisiert dann list, um auf n zu zeigen. Derselbe Vorgang wird für 2 wiederholt. Als nächstes erzeugt node *ptr = list eine temporäre Variable, die auf die gleiche Stelle zeigt, auf die list zeigt. Das while gibt aus, auf welchen Knoten ptr zeigt, und aktualisiert dann ptr so, dass es auf den next-Knoten in der Liste zeigt. Schließlich wird der gesamte Speicher freigegeben.

In diesem Beispiel erfolgt das Einfügen in die Liste immer in $O(1)$, da es nur eine sehr geringe Anzahl von Schritten erfordert, am Anfang einer Liste einzufügen.
Der Zeitaufwand für das Durchsuchen dieser Liste liegt in der Größenordnung von $O(n)$, da im schlimmsten Fall immer die gesamte Liste durchsucht werden muss, um ein Element zu finden. Die Zeitkomplexität für das Hinzufügen eines neuen Elements zur Liste hängt davon ab, wo das Element hinzugefügt wird. Dies wird in den folgenden Beispielen veranschaulicht.
Verknüpfte Listen werden nicht in einem zusammenhängenden Speicherblock gespeichert. Sie können beliebig groß werden, vorausgesetzt, dass genügend Systemressourcen vorhanden sind. Der Nachteil ist jedoch, dass mehr Speicher benötigt wird, um die Liste zu verwalten als ein Array. Das liegt daran, dass Sie für jedes Element nicht nur den Wert des Elements, sondern auch einen Pointer auf den nächsten Knoten speichern müssen. Außerdem kann in verknüpften Listen nicht wie bei einem Array direkt “hineinindiziert” werden. Es ist also nicht möglich, beispielsweise direkt auf das fünfte Element zuzugreifen. Stattdessen muss man alle vorherigen $n-1$ Elemente anwandern und den Pointern folgen, um die Position und den Inhalt des fünften Elements zu finden. Aus diesem Grund muss die oben abgebildete Liste linear durchsucht werden. Eine binäre Suche ist daher in einer so konstruierten Liste nicht möglich.

Natürlich könnten Sie auch, wie in diesem Code dargestellt, Zahlen an das Ende der Liste anfügen (Code wurde in der Vorlesung nicht gezeigt):

// Implementiert eine Liste von Zahlen mit Hilfe einer verknüpften Liste

#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct node
{
    int number;
    struct node *next;
}
node;

int main(int argc, char *argv[])
{
    node *list = NULL;

    // Für jedes Befehlszeilenargument
    for (int i = 1; i < argc; i++)
    {
        // Argument in int umwandeln
        int number = atoi(argv[i]);

        // Knoten für Nummer zuweisen
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = number;
        n->next = NULL;

        // Wenn die Liste leer ist
        if (list == NULL)
        {
            // Dieser Knoten ist die gesamte Liste
            list = n;
        }

        // Wenn die Liste bereits Zahlen enthält
        else
        {
            // Iterieren über Knoten in der Liste
            for (node *ptr = list; ptr != NULL; ptr = ptr->next)
            {
                // Falls am Ende der Liste
                if (ptr->next == NULL)
                {
                    // Knoten anhängen
                    ptr->next = n;
                    break;
                }
            }
        }
    }

    // Zahlen ausgeben
    for (node *ptr = list; ptr != NULL; ptr = ptr->next)
    {
        printf("%i\n", ptr->number);
    }

    // Speicher freigeben
    node *ptr = list;
    while (ptr != NULL)
    {
        node *next = ptr->next;
        free(ptr);
        ptr = next;
    }
}

Beachten Sie, wie dieser Code die Liste abläuft, um das Ende zu finden. Beim Anhängen eines Elements (Hinzufügen am Ende der Liste) läuft unser Code in $O(n)$, da wir unsere gesamte Liste durchgehen müssen, bevor wir das letzte Element hinzufügen können.

Wenn wir eine Liste sortieren wollen, gelingt das am einfachsten in dem Moment, in dem neue Einträge hinzugefügt werden. Wir müssen dann das neue Element an der richtigen Stelle einhängen. Dazu müssen wir die Liste “auftrennen” und die next-Pointer des Vorgängers und des neuen Knotens korrekt setzen (Code wurde in der Vorlesung nicht gezeigt):

// Implementiert eine sortierte Liste von Zahlen unter Verwendung einer verketteten Liste

#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct node
{
    int number;
    struct node *next;
}
node;

int main(int argc, char *argv[])
{
    // Speicher für Zahlen
    node *list = NULL;

    // Für jedes Befehlszeilenargument
    for (int i = 1; i < argc; i++)
    {
        // Argument in int umwandeln
        int number = atoi(argv[i]);

        // Knoten für Nummer zuweisen
        node *n = malloc(sizeof(node));
        if (n == NULL)
        {
            return 1;
        }
        n->number = number;
        n->next = NULL;

        // Wenn die Liste leer ist
        wenn (list == NULL)
        {
            Liste = n;
        }

        // Wenn die Zahl am Anfang der Liste steht
        else if (n->number < list->number)
        {
            n->nächste = list;
            list = n;
        }

        // Wenn die Nummer weiter hinten in der Liste steht
        else
        {
            // Iterieren über Knoten in der Liste
            for (node *ptr = list; ptr != NULL; ptr = ptr->next)
            {
                // Falls am Ende der Liste
                if (ptr->next == NULL)
                {
                    // Knoten anhängen
                    ptr->next = n;
                    break;
                }

                // Wenn in der Mitte der Liste
                if (n->number < ptr->next->number)
                {
                    n->next = ptr->next;
                    ptr->next = n;
                    break;
                }
            }
        }
    }

    // Zahlen ausgeben
    for (node *ptr = list; ptr != NULL; ptr = ptr->next)
    {
        printf("%i\n", ptr->number);
    }

    // Speicher freigeben
    node *ptr = list;
    while (ptr != NULL)
    {
        node *next = ptr->next;
        free(ptr);
        ptr = next;
    }
}

Beachten Sie, wie diese Liste beim Aufbau sortiert wird. Um ein Element in dieser speziellen Reihenfolge einzufügen, wird unser Code immer noch bei jedem Einfügen durchlaufen, da wir im schlimmsten Fall alle aktuellen Elemente durchsuchen müssen. Die Laufzeit ist in der Größenordnung von $O(n)$.

Schauen Sie sich das Short-Video zu Verketteten Listen an. Dort werden die Operationen (create, find, insert, destroy und delete) anhand von Beispielen ausführlich erklärt.

Bäume

Binäre Suchbäume sind eine weitere Datenstruktur, die verwendet werden kann, um Daten effizienter zu speichern, so dass sie durchsucht und abgerufen werden können.
Sie können sich eine sortierte Folge von Zahlen vorstellen.

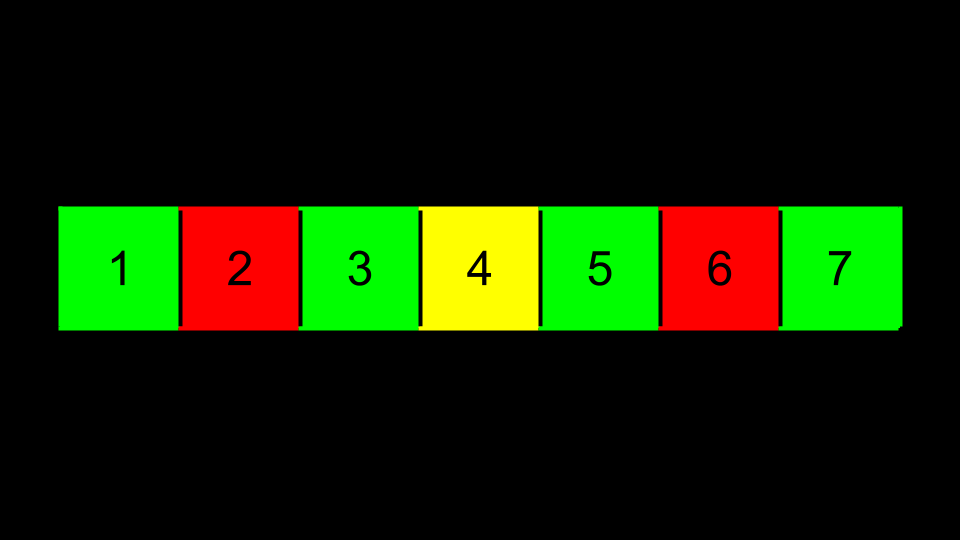
Baum
Stellen Sie sich also vor, dass der mittlere Wert die Spitze eines Baumes ist. Die Werte, die kleiner als dieser Wert sind, werden nach links gestellt. Die Werte, die größer als dieser Wert sind, liegen rechts.

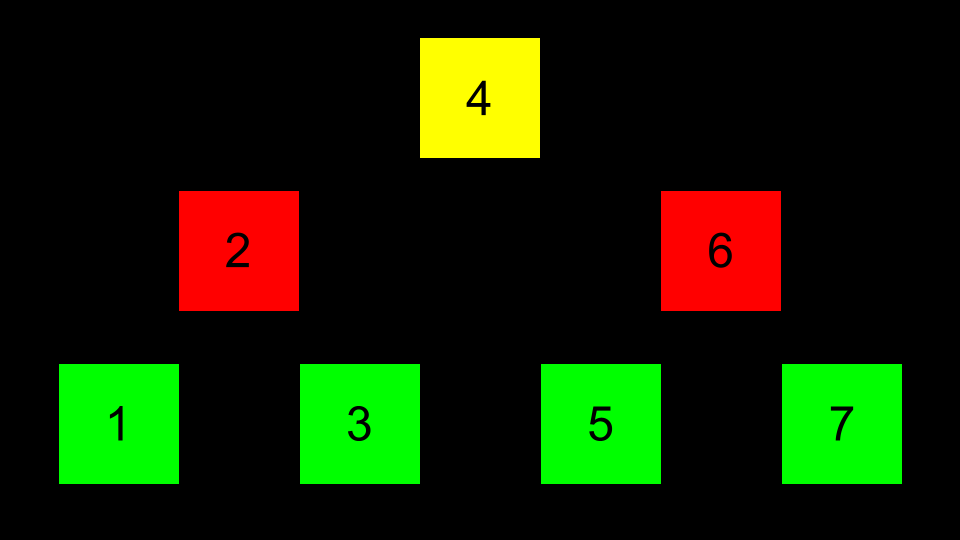
Baum
Dann können Pointer verwendet werden, um auf die richtige Stelle jedes Speicherbereichs zu zeigen, so dass jeder dieser Knotenpunkte verbunden werden kann.

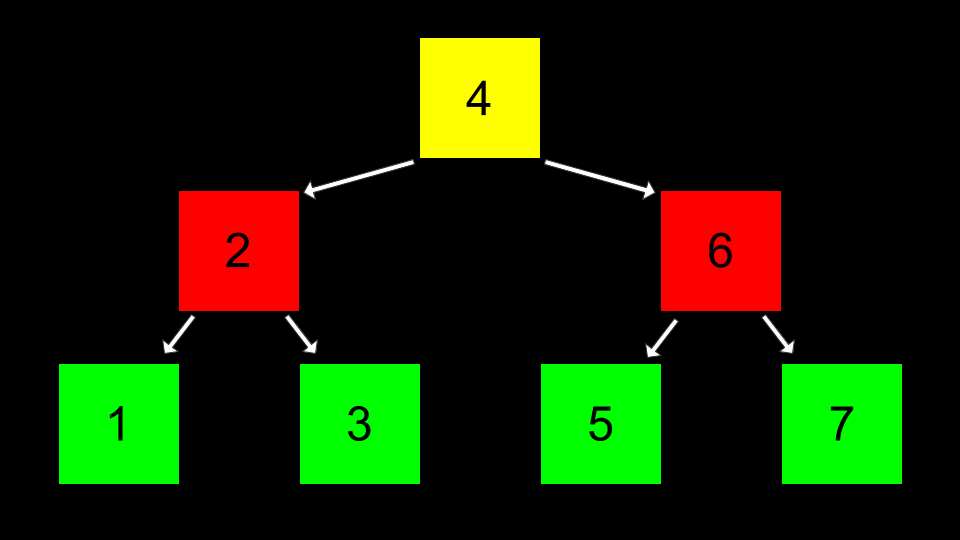
Baum

Eine Suche nach einer Zahl lässt sich wie folgt implementieren:

bool search(node *tree, int number)
{
    if (tree == NULL)
    {
        return false;
    }
    else if (number < tree->number)
    {
        return search(tree->left, number);
    }
    else if (number > tree->number)
    {
        return search(tree->right, number);
    }
    else if (number == tree->number)
    {
        return true;
    }
}

Beachten Sie, dass eine Suchfunktion bei diesem Baum zunächst den Ort tree aufsucht. Dann verwendet sie eine Rekursion, um nach number zu suchen. Die Funktion free_tree gibt den Baum rekursiv frei. Die Funktion print_tree gibt den Baum rekursiv aus.

Ein Baum wie der obige bietet eine Dynamik, die ein Array nicht bieten kann. Er kann wachsen und schrumpfen, wie wir wollen.
Außerdem bietet diese Struktur eine Suchzeit von $O(\mathrm{log}~n)$.
Allerdings gilt dies nur im Idealfall eines balancierten Baums, wenn wir die Elemente in ungünstiger Reihenfolge in den Baum einfügen (z.B. wenn die Elemente bereits sortiert sind), dann entsteht ein unbalancierter Baum (siehe Vorlesungsfolien) – de facto haben wir dann eine Verkettete Liste erzeugt, sodass wir von den Vorteilen der Baumstruktur nichts haben. In weiterführenden Kursen über Datenstrukturen werden Sie Verfahren kennenlernen, mit denen Sie einen unbalancierten Baum wieder “rebalancieren” können.

Dictionaries

Eine weitere Datenstruktur sind Dictionaries (Wörterbücher).
So wie echte Wörterbücher in Buchform, die ein Wort und eine Definition haben, haben Dictionaries Paare aus “Keys” (Schlüssel) und “Values” (Wert).
Der heilige Gral der algorithmischen Zeitkomplexität ist $O(1)$ oder konstante Zeit. Das heißt, der ultimative Anspruch ist, dass der Zugriff sofort erfolgt.

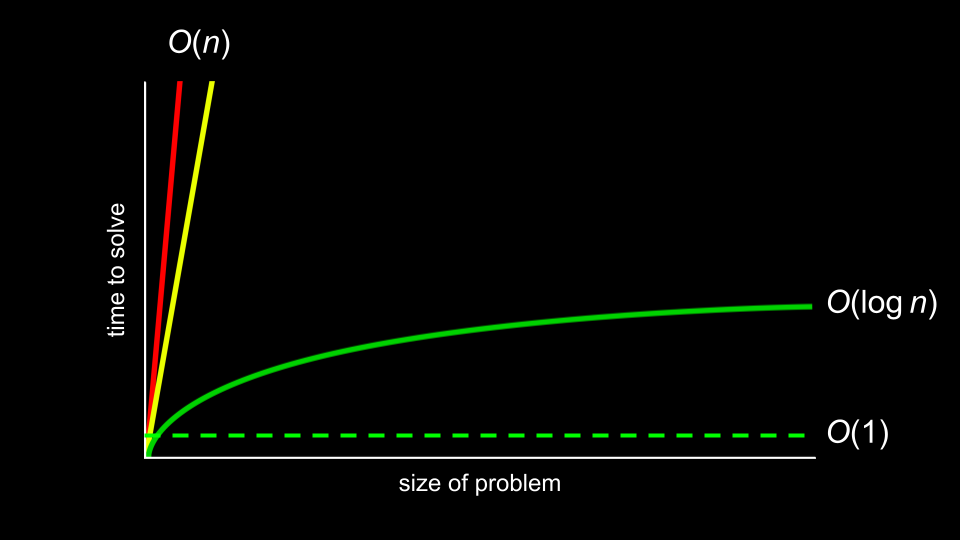
time complexity
Wörterbücher können diese Zugriffsgeschwindigkeit durch Hashing bieten.

Hashing und Hash-Tabellen

Unter Hashing versteht man die Idee, einen Wert zu nehmen und einen Wert auszugeben, der später eine Abkürzung dafür ist.
Eine Hashfunktion ist ein Algorithmus, der einen beliebigen großen Wert auf einen kleinen (vorhersehbaren) Wert reduziert.
Wir haben gesehen, dass man die Suche nach einer von 52 Spielkarten beschleunigen kann, indem man die Karten zuerst anhand ihrer Farbwerte aufteilt (in Buckets) legt. Dann muss man später nur ein Viertel durchsuchen, wenn man nach einer konkreten Karte sucht. Das ist die Grundidee von Hash-Tabellen.
Zum Beispiel könnte eine Hashfunktion für den String apple den Hashwert (kurz oft als Hash bezeichnet) 1 errechnen, während berry vielleicht zu einer 2 gehasht würde. Die Hashwerte nutzt man dann um die Speicherorte der Strings festzulegen.
Dann kann man den Eintrag von apple schnell im Speicher finden – man muss nur den Hash-Algorithmus nach dem Hashwert von apple fragen. Der gibt dann an, wo apple zu finden ist.
Auch wenn es vom Design her nicht ideal ist, alle a in den einen Eimer und alle b in einen anderen zu legen, ist dieses Konzept der Bucketisierung anhand von gehashten Werten verbreitet: Die Hashwerte der Einträge werden verwendet, um die Suche danach abzukürzen.
Man kann beispielsweise eine Hashfunktion nutzen, um für die zu speichernden Elemente die Hashwerte zu ermitteln. Die Elemente selbst speichert man in einer Hash-Tabelle ab. Die Hashfunktion ist so konstruiert, dass sie für jedes Element eine ganze Zahl zurückgibt. Diese wird als Array-Index genutzt und legt fest, wo im Array (bzw. in der Hash-Tabelle) das Element eingefügt werden soll.
Eine Hash-Tabelle ist eine clevere Kombination aus Arrays und verknüpften Listen. Wenn sie in Code implementiert wird, ist eine Hash-Tabelle ein Array von Pointern auf Knoten.
Eine Hash-Tabelle könnte man sich wie folgt vorstellen:

alphabet

Beachten Sie, dass es sich um ein Array handelt, dem jeder Wert des Alphabets zugewiesen wird.
Dann wird an jeder Stelle des Arrays eine verkettete Liste verwendet, um jeden Wert zu verfolgen, der dort gespeichert wird:

alphabet
Kollisionen treten auf, wenn Sie der Hash-Tabelle Werte hinzufügen und an der Hash-Position bereits etwas vorhanden ist. Im obigen Beispiel werden Kollisionen einfach an die Verkettete Liste angehängt. Kollisionen sind unerwünscht, weil sie zu höherer Laufzeit führen – schließlich müssen wir dann die jeweilige Verkettete Liste traversieren um das Element zu finden.
Kollisionen können durch eine bessere Programmierung der Hash-Tabelle und des Hash-Algorithmus reduziert werden. Sie können sich eine Verbesserung des obigen Beispiels wie folgt vorstellen:

alphabet
Wir könnten also die Buchstaben wie ein Stellenwertsystem zur Basis 26 interpretieren (siehe Short-Video Hexadezimal) und dann die Position im Array ermitteln. Verwendet man als Hash die ersten drei Buchstaben, gibt es $26^3 = 17576$ Elemente im Array.
Betrachten Sie das folgende Beispiel für einen Hash-Algorithmus:

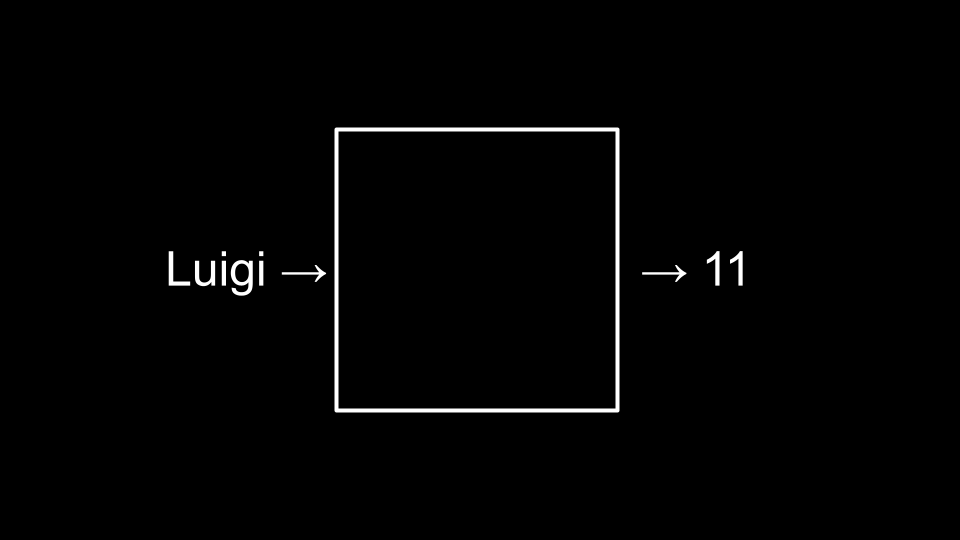
hashing
Dies könnte in Code umgesetzt werden als:
```
#include <ctype.h>

unsigned int hash(const char *word)
{
    return toupper(wort[0]) - 'A';
}
```
Wie Sie sehen gibt die Hash-Funktion den Wert von toupper(word[0]) - 'A' zurückgibt. Diese Konstruktion wandelt den ersten Buchstaben von word in einen Großbuchstaben um und zieht anschließend den ASCII-Wert von 'A' ab. Dadurch wird der Buchstabe in eine Zahl zwischen 0 und 25 umgewandelt.
Beachten Sie, dass wir in dieser Funktion den Parameter word den Modifier const verwendet haben. Es ist guter Stil, dies immer dann zu tun, wenn eine Funktion eine Variable als Referenz übergeben bekommt (also einen Pointer oder ein Array als Parameter hat), aber wir in der Funktion nicht beabsichtigen, die Werte zu ändern. Dies ist hier der Fall, wir wollen auf word ja nur lesend zugreifen. Mit const informieren wir den Compiler über unsere Absicht. Sollten wir den Pointer (versehentlich) dereferenzieren und den Wert der Variable ändern, gibt der Compiler eine Fehlermeldung aus.
Weiterhin ist Ihnen vielleicht aufgefallen, dass wir unsigned int als Rückgabewert verwenden. Auch dies ist guter Stil, der Fehler vermeidet. Den Rückgabewert der hash-Funktion beabsichtigen wir ja als Index für unsere Hashtabelle zu verwenden. Dabei handelt es sich um ein Array – und in Arrays sind nur positive Zahlen als Index erlaubt. Indem wir unsigned verwenden, machen wir dies im Code sichtbar und der Compiler wird Fehlermeldungen ausgeben, wenn wir versuchen, den Rückgabewert einer vorzeichenbehafteten int-Variable zuzuweisen. Dadurch werden schwer findbare Laufzeitfehler vermieden.
Als Programmierer müssen Sie entscheiden, ob es vorteilhafter ist, mehr Speicher für eine große Hash-Tabelle zu verwenden und damit die Suchzeit zu verkürzen (im Idealfall bis hinunter zu $O(1)$, wenn so viele Einträge vorhanden sind, dass es zu keinen Kollisionen kommt) oder weniger Speicher zu verwenden und damit die Suchzeit zu erhöhen.

Tries

Tries sind eine weitere abstrakte Datenstruktur, mit der man ein Dictionary implementieren kann (siehe Vorlesungsfolien).
Bei Tries bauen wir eine Baumstruktur aus Arrays.
Der größte Vorteil: Tries sind immer in konstanter Zeit durchsuchbar, also $O(1)$.
Aber: Tries benötigen dafür vergleichsweise viel Speicherplatz. Beachten Sie, dass wir Knoten $26 \cdot 4 = 104$ Knoten brauchen, nur um toad zu speichern!
toad würde wie folgt gespeichert werden:

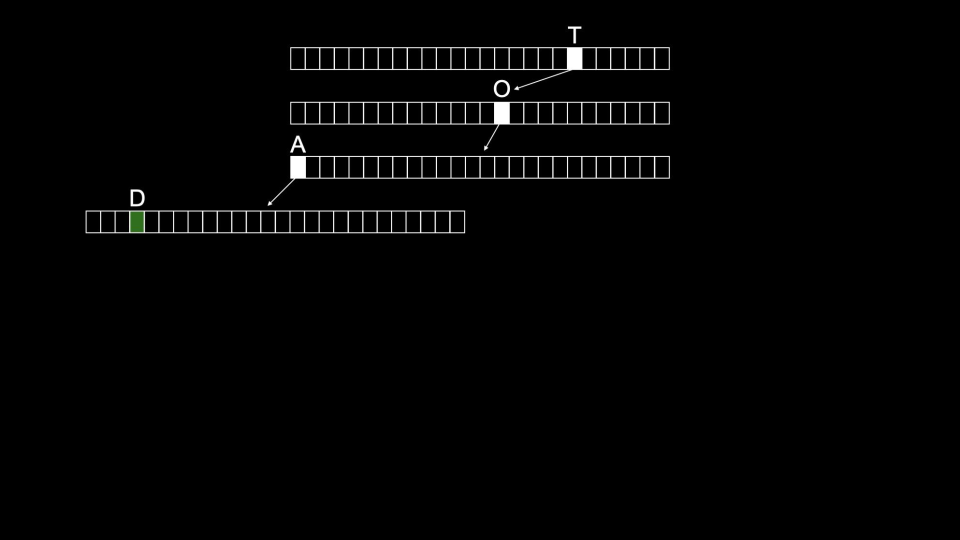
tries
Tom würde dann wie folgt gespeichert werden:

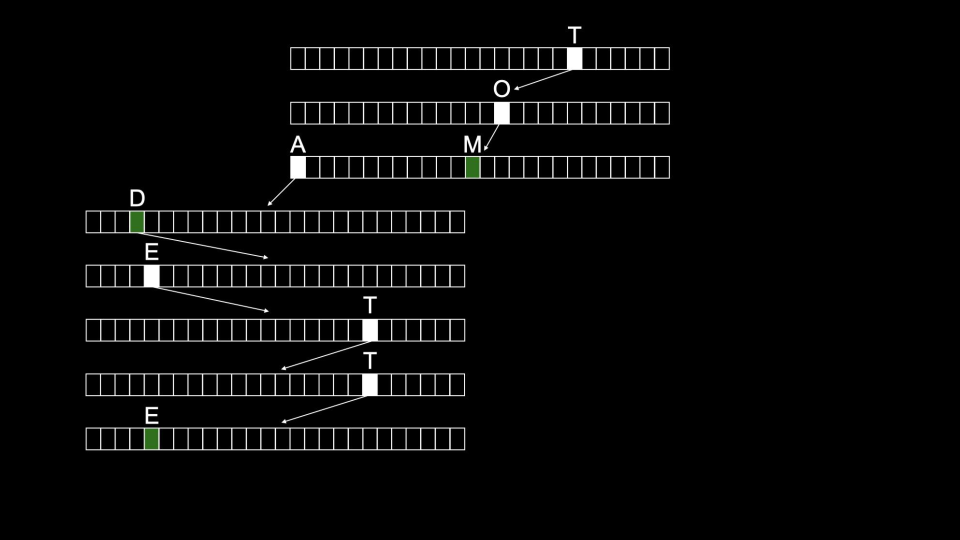
tries
Den Key speichern wir also nicht explizit im Trie, sondern implizit in den Pfaden, die wir zur Suche durchlaufen.
Beachten Sie, dass Wörter mit gleichen Wortanfängen denselben Pfad durch den Trie verwenden.
Die Komplexität der Suche ist $O(1)$, da sie unabhängig von der Anzahl der Elemente im Trie ist. Für ein konkretes Element ist die Anzahl der Schritte immer gleich – unabhängig davon wie viele andere Elemente noch in der Datenstruktur gespeichert sind.
Schauen Sie sich das Short-Video zu Tries an, das noch ein weiteres Beispiel zeigt und eine speicherplatzoptimierte Variante erklärt.

Zusammenfassend

In dieser Lektion haben Sie die Verwendung von Pointern zum Aufbau neuer Datenstrukturen kennen gelernt. Insbesondere behandelt haben mit…

Pointer auf structs und dem Pfeil-Operator
Queues und Stacks
Verkettete Listen
Dictionaries und Hashing
Tries

Bis zum nächsten Mal!

5.1 Strukturen