Notes 3

Sie können diese Seite ausdrucken oder mit einem PDF-Drucker in ein PDF umwandeln, um Ihre eigenen Notizen hinzuzufügen.

Willkommen!

• In Woche 0 haben wir die Idee eines Algorithmus eingeführt: eine Blackbox, die eine Eingabe entgegennehmen und eine Ausgabe erzeugen kann.

• In dieser Woche werden wir unser Verständnis von Algorithmen durch Pseudocode und Code erweitern.

• Außerdem werden wir uns mit der Effizienz von Algorithmen befassen. Und wir werden die Programmierkonstrukte, die wir in den letzten Wochen gesehen haben zur Erstellung von Algorithmen verwenden.

• Erinnern Sie sich an den Anfang des Kurses, als wir uns das folgende Diagramm angesehen haben:

  

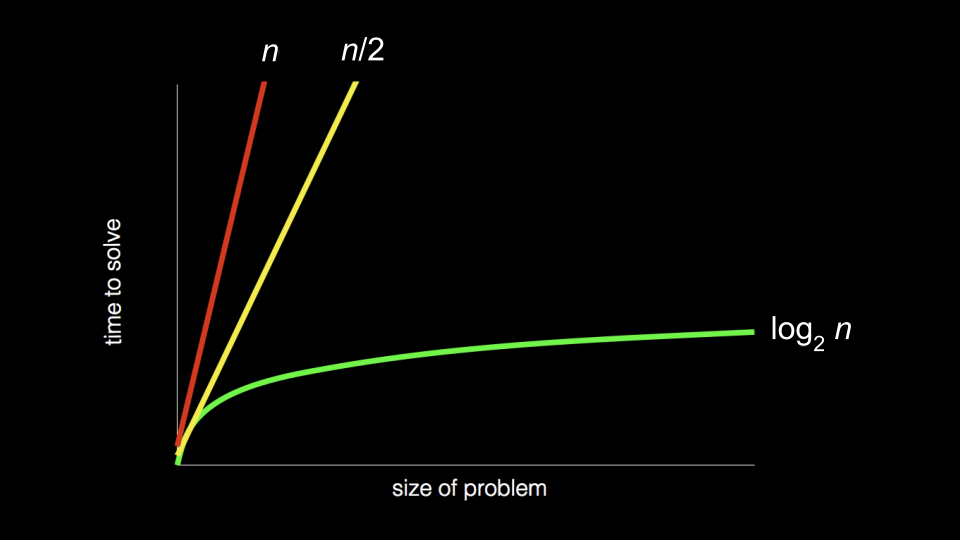
• In dieser Woche werden wir sehen, wie die Art und Weise, wie ein Algorithmus mit einem Problem arbeitet, die Zeit bestimmen kann, die er zur Lösung eines Problems benötigt. Algorithmen können – bis zu einer gewissen Grenze – immer effizienter gestaltet werden.

Lineare Suche

• Erinnern Sie sich an die Idee eines Arrays, d.h. Speicherblöcke, die aufeinander folgen: Seite an Seite mit anderen.

• Sie können sich ein Array metaphorisch wie eine Reihe von Fächern vorstellen.

• Nehmen wir an, in jedem Fach liegt ein Zettel mit einer Zahl und wir wollen wissen: “Ist die Zahl 50 in einem der Fächer?“ So wie wir muss ein Computer jedes Fach der Reihe nach anschauen, um herauszufinden, ob sich die Zahl 50 darin befindet. Zu ermitteln, ob ein bestimmtes Element im Array enthalten ist oder nicht, ist ein Standard-Problem der Informatik, die Suche.

• Wir können unser Array an einen Such-Algorithmus übergeben, der es durchsucht, um zu sehen, ob sich die Zahl 50 in einem der Fächer befindet. Der Algorithmus gibt entweder true oder false zurück.

• Um diese Aufgabe zu bewältigen könnte der Algorithmus in etwa so vorgehen:

  Für jedes Fach von links nach rechts
      Wenn 50 im Fach ist
          Rückgabe true
  Rückgabe false

  Die obigen Anweisungen sind Pseudocode: Eine für Menschen lesbare Version der Anweisungen.

• Eine Informatikerin oder ein Informatiker würde den Pseudocode vielleicht wie folgt aufschreiben:

  For i from 0 to n-1
      If 50 in boxes[i]
          Return true
  Return false

  Beachten Sie, dass es sich bei der obigen Darstellung noch nicht um Code handelt, aber es ist schon eine ziemlich gute Annäherung an den endgültigen Code.

Binäre Suche

• Die Binäre Suche ist ein weiterer Suchalgorithmus, der bei unserer Aufgabe, die 50 zu finden, eingesetzt werden könnte.

• Unter der Annahme, dass die Werte in den Schränken vom kleinsten zum größten Wert geordnet sind, würde der Pseudocode für die binäre Suche wie folgt aussehen:

  Wenn keine Fächer mehr vorhanden sind
      Rückgabe false
  Wenn 50 hinter im mittleren Fach ist
      Rückgabe true
  Sonst wenn 50 < Wert im mittleren Fach
      Linke Hälfte durchsuchen
  Sonst wenn 50 > Wert im mittleren Fach
      Rechte Hälfte durchsuchen

• Wenn wir die Array-Schreibweise nutzen, würde der Pseudocode so aussehen:

  If no boxes left
      Return false
  If 50 is behind boxes[middle]
      Return true
  Else if 50 < boxes[middle]
      Search boxes[0] through boxes[middle - 1]
  Else if 50 > boxes[middle]
      Search boxes[middle + 1] through boxes[n - 1]

  Diese Annäherung an den Code zeigt schon ganz gut, wie man die Binäre Suche programmieren würde.

Laufzeit

• Wenn wir Algorithmen hinsichtlich ihrer Effizienz im Hinblick auf ihre Laufzeit analysieren, erfolgt dies in der Regel mit der O-Notation. Werfen Sie einen Blick auf das folgende Diagramm:

  

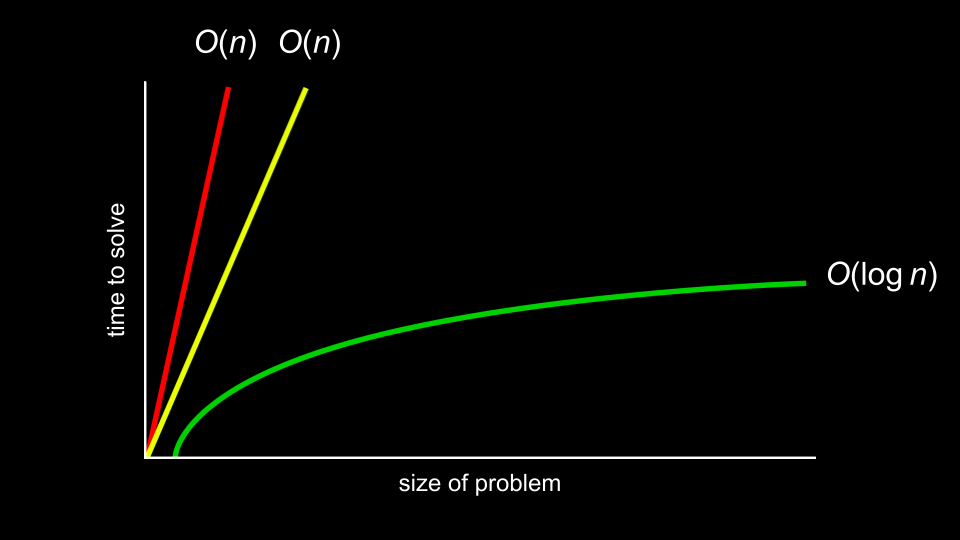
• Anstatt die Laufzeit eines Algorithmus ganz genau zu messen, interessieren wir uns in der Informatik eher für die Ordnung der verschiedenen Laufzeiten.

• In der obigen Grafik hat der erste Algorithmus eine Laufzeit von der Ordnung von n. Der zweite läuft ebenfalls in linearer Zeit. Beim dritten ist die Laufzeit von logarithmischer Ordnung.

• Es ist die Form der Kurve, die die Effizienz eines Algorithmus zeigt.

• Bei den oben genannten Laufzeiten betrachten wir immer den Worst Case, also wenn wir kein Glück haben.

• Die lineare Suche benötigt im schlechtesten Fall n Schritte.

• Die binäre Suche ist im schlechtesten Fall besser als die lineare Suche, weil sie auch im ungünstigsten Fall immer weniger Schritte benötigt.

• Wir interessieren uns sowohl für den schlechtesten Fall (Obergrenze) als auch für den besten Fall (Untergrenze).

• Das Symbol Ω (Omega) wird verwendet, um den besten Fall eines Algorithmus zu kennzeichnen.

• In anderen Kursen werden Sie sich detaillierter mit der Komplexität von Algorithmen befassen.

search.c

• Sie können eine lineare Suche implementieren, indem Sie code search.c in Ihr Terminalfenster eingeben und folgenden Code schreiben:

  #include <cs50.h>
  #include <stdio.h>
  
  int main(void)
  {
      int numbers[] = {20, 500, 10, 5, 100, 1, 50};
  
      int n = get_int("Zahl: ");
      for (int i = 0; i < 7; i++)
      {
          if (numbers[i] == n)
          {
              printf("Found\n");
          }
          else
          {
              printf("Not found\n");
          }
      }
  }

  Dieser Code hat einen Bug, oder? Vielleicht sollten wir es nicht mit if-else programmieren.

  #include <cs50.h>
  #include <stdio.h>
  
  int main(void)
  {
      int numbers[] = {20, 500, 10, 5, 100, 1, 50};
  
      int n = get_int("Zahl: ");
      for (int i = 0; i < 7; i++)
      {
          if (numbers[i] == n)
          {
              printf("Found\n");
          }
      }
      printf("Not found\n");
  }

  Dieser Code hat auch noch einen Bug. Wie können wir das besser machen? Wir müssen die Schleife vorzeitig verlassen, wenn wir die Zahl gefunden haben.

  #include <cs50.h>
  #include <stdio.h>
  
  int main(void)
  {
      int numbers[] = {20, 500, 10, 5, 100, 1, 50};
  
      int n = get_int("Zahl: ");
      for (int i = 0; i < 7; i++)
      {
          if (numbers[i] == n)
          {
              printf("Found\n");
              return 0;
          }
      }
      printf("Not found\n");
      return 1;
  }

  Beachten Sie, dass die Zeile, die mit int numbers[] beginnt, es uns ermöglicht, die Werte der einzelnen Elemente des Arrays zu initialisieren – die Länge ermittelt der Compiler automatisch. Weiterhin haben wir in der for-Schleife eine Implementierung der linearen Suche. Mit return 0 wird der Erfolgsfall angezeigt und das Programm beendet. return 1 wird verwendet, um das Programm mit einem Fehler zu beenden. Der Grund, warum man 0 für den Erfolgsfall nimmt, ist, dass es in der Regel nur einen Erfolgsfall gibt, aber mehrere mögliche Fehlerzustände. Nimmt man die 0 für den Erfolgsfall kann man alle übrigen Zahlen für die verschiedenen Fehlerzustände verwenden.

• Wir haben nun selbst eine lineare Suche in C implementiert!

• Was wäre, wenn wir nach einer Zeichenkette innerhalb eines Arrays suchen wollten? Ändern Sie Ihren Code wie folgt:

  #include <cs50.h>
  #include <stdio.h>
  
  int main(void)
  {
      string strings[] = {"Schiff", "Auto", "Hund", "Katze", "Hut"};
  
      string s = get_string("String: ");
      for (int i = 0; i < 6; i++)
      {
          if (strings[i] == 0)
          {
              printf("Gefunden\n");
              return 0;
          }
      }
      printf("Nicht gefunden\n");
      return 1;
  }

  Beachten Sie, dass wir dieses Mal nicht == verwenden können, wie im vorigen Programms. Stattdessen verwenden wir strcmp, das aus der Bibliothek string.h stammt. strcmp” gibt “0” zurück, wenn die Zeichenketten gleich sind.

  #include <cs50.h>
  #include <stdio.h>
  #include <string.h>
  
  int main(void)
  {
      string strings[] = {"Schiff", "Auto", "Hund", "Katze", "Hut"};
  
      string s = get_string("String: ");
      for (int i = 0; i < 6; i++)
      {
          if (strcmp(strings[i], s) == 0)
          {
              printf("Gefunden\n");
              return 0;
          }
      }
      printf("Nicht gefunden\n");
      return 1;
  }

• Warum ist es clever, dass strcmp den Wert 0 zurückgibt? Nun, strmcp prüft die Strings nicht nur auf Gleichheit, sondern vergleicht sie hinsichtlich ihrer ASCII-betischen Reihenfolge (nützlich, falls Sie Strings sortieren möchten).

• Wenn wir diesen Code ausführen, iterieren wir über das Array von Zeichenketten, um prüfen, ob eine bestimmte Zeichenkette darin enthalten ist. Wenn Sie einen Segmentation Fault sehen, hat Ihr Programm einen Teil des Speichers berührt, auf den es keinen Zugriff haben sollte. Vergewissern Sie sich dann, dass Sie “i < 6” und nicht “i < 7” verwendet haben.

• Wir können diese Ideen von Zahlen und Zeichenketten in einem einzigen Programm kombinieren. Geben Sie code phonebook.c in Ihr Terminalfenster ein und schreiben Sie folgenden Code:

  #include <cs50.h>
  #include <stdio.h>
  #include <string.h>
  
  int main(void)
  {
      string names[] = {"Dominik", "Bittle", "Office"};
      string numbers[] = {"+49-951-863-2661", "+49-951-863-2661", "+49-951-863-2795"};
  
      string name = get_string("Name: ");
      for (int i = 0; i < 3; i++)
      {
          if (strcmp(names[i], name) == 0)
          {
              printf("Found %s\n", numbers[i]);
              return 0;
          }
      }
      printf("Not found\n");
      return 1;
  }

  Beachten Sie, dass wir für die Telefonnummern keinen Integer- sondern einen String-Datentyp verwenden, weil wir nicht nur Ziffern, sondern auch Sonderzeichen speichern wollen. Dominiks und Bittles Telefonnummern sind numbers[0] bzw. numbers[1]. Das Office hat die Nummer -2795, also numbers[2]. Das Programm erlaubt es uns, ein einfaches Telefonbuch nach der Nummer einer bestimmten Person zu durchsuchen.

• Das Design des Programms ist schlecht (man nennt so etwas auch Code Smell). Name und Nummer stehen in getrennten Arrays – es könnte passieren. Würden wir z.B. nur die Namensliste sortieren, müssten wir daran denken, die Telefonnummern auch entsprechend zu sortieren – sonst passt die Zuordnung über den Index nicht mehr.

• Wäre es nicht schön, wenn wir einen eigenen Datentyp erstellen könnten, mit dem wir eine Person mit einer Telefonnummer verknüpfen können?

structs

• In C gibt es eine Möglichkeit, eigene Datentypen zu erstellen.

• Wir können damit einen eigenen Datentyp namens “Person” erstellen, der zwei Informationen aufnimmt: “Name” und eine “Nummer”.

• Ändern Sie Ihren Code dazu wie folgt:

  #include <cs50.h>
  #include <stdio.h>
  #include <string.h>
  
  typedef struct
  {
      string name;
      string number;
  }
  person;
  
  int main(void)
  {
      person people[3];
  
      people[0].name = "Dominik";
      people[0].number = "+49-951-863-2661";
  
      people[1].name = "Bittle";
      people[1].number = "+49-951-863-2661";
  
      people[2].name = "Office";
      people[2].number = "+49-951-863-2795";
  
      string name = get_string("Name: ");
      for (int i = 0; i < 3; i++)
      {
          if (strcmp(people[i].name, name) == 0)
          {
              printf("Gefunden %s\n", people[i].number);
              return 0;
          }
      }
      printf("Nicht gefunden\n");
      return 1;
  }

  Beachten Sie, dass der Code mit typedef struct beginnt, wo ein neuer Datentyp namens person definiert wird. Innerhalb einer person befindet sich ein String namens name und ein String namens number. In der Funktion main beginnen wir mit der Erstellung eines Arrays namens people, das vom Typ person ist und eine Größe von 3 hat. Dann aktualisieren wir die Namen und Telefonnummern der beiden Personen in unserem people-Array. Beachten Sie vor allem, dass die Punktschreibweise, z. B. people[0].name, es uns ermöglicht, auf die Person an der 0-ten Stelle zuzugreifen und dieser Person einen Namen zuzuweisen.

Selection Sort

• Beim Sortieren wird eine unsortierte Liste von Werten in eine sortierte Liste umgewandelt.

• Wenn eine Liste sortiert ist, ist die Suche in dieser Liste für den Computer weit weniger anstrengend. Erinnern Sie sich daran, dass wir die binäre Suche auf eine sortierte Liste anwenden können, aber nicht auf eine unsortierte Liste.

• Es gibt viele verschiedene Sortieralgorithmen.

• Selection Sort ein solcher Suchalgorithmus.

• Der Algorithmus für Selection Sort lautet in Pseudocode:

  Für i von 0 bis n-1
      Suche kleinste Zahl zwischen Zahlen[i] und Zahlen[n-1]
      Tausche kleinste Zahl mit Zahlen[i]

• Fasst man diese Schritte zusammen, so dauerte die erste Iteration durch die Liste n - 1 Schritte. Das zweite Mal dauerte es n - 2 Schritte. Führt man diese Logik fort, lassen sich die erforderlichen Schritte wie folgt darstellen:

  (n - 1) + (n - 2) + (n - 3) + ... + 1

• Dieser Ausdruck lässt sich vereinfachen zu n (n-1) / 2.

• Dabei ist $n^2$ wirklich der einflussreichste Faktor bei der Bestimmung der Effizienz dieses Algorithmus. Daher hat Selection Sort im ungünstigsten Fall, wenn alle Werte unsortiert sind, eine Laufzeit der Größenordnung $O(n^2)$.

• Selbst wenn alle Werte sortiert sind, wird die gleiche Anzahl von Schritten benötigt. Daher kann der beste Fall wie folgt notiert werden: $\Omega(n^2)$.

Bubble Sort

• Bubble Sort ist ein weiterer Sortieralgorithmus, der durch wiederholtes Vertauschen von Elementen größere Elemente an das Ende aufsteigen lässt – so wie Luftblasen im Wasserglas aufsteigen.

• Der Pseudocode für Bubble Sort lautet:

  n-1 Mal wiederholen
      Für i von 0 bis n-2
          Wenn Zahlen[i] und Zahlen[i+1] nicht in der richtigen Reihenfolge sind
              Vertausche sie
      Wenn keine Vertauschung
          Beenden

• Wenn wir das Array nach und nach sortieren, wissen wir, dass immer mehr davon sortiert sein wird, so dass wir uns nur die Zahlenpaare ansehen müssen, die noch nicht sortiert wurden.

• Bei der Analyse von Bubble Sort haben wir die äußere Schleife n - 1 mal und die innere Schleife ebenfalls n - 1 mal durchlaufen. Wenn man dies mathematisch darstellt, wobei n die Anzahl der Fälle darstellt, sieht man, dass sich die Anzahl der Schleifendurchläufe bei Bubble Sort im Worst Case wie folgt berechnen lässt:

    (n – 1) · (n – 1)

  oder, einfacher ausgedrückt, $O(n^2)$.

• Im besten Fall ist die Laufzeit hingegen $\Omega(n)$.

• Ein visueller Vergleich dieser Algorithmen findet sich online.

Rekursion

• Wie können wir unsere Effizienz beim Sortieren verbessern?

• Rekursion ist ein Konzept in der Programmierung, bei dem eine Funktion sich selbst aufruft. Wir haben das bereits gesehen, als wir gesucht haben.

  Wenn keine Fächer mehr vorhanden sind
      Rückgabe false
  Wenn Nummer im mittleren Fach ist
      Rückgabe true
  Sonst wenn Zahl < Wert im mittleren Fach
      Linke Hälfte suchen
  Sonst wenn Zahl > Wert im mittleren Fach
      Rechte Hälfte durchsuchen

  Beachten Sie, dass wir die Suche auf immer kleineren Varianten des Problems aufrufen.

• Auch in unserem Pseudocode für Woche 0 gibt es schon Bezüge zur Rekursion:

  1   Nimm Telefonbuch
  2   Öffne das Telefonbuch in der Mitte
  3   Schau dir die Seite an.
  4   Wenn die Person auf der Seite ist
  5       Rufe die Person an.
  6   Oder wenn die Person weiter vorne steht
  7       Gehe zur Mitte der linken Hälfte
  8       Gehe zurück zu Zeile 3
  9   Oder wenn die Person weiter hinten steht
  10      Gehe zur Mitte der rechten Hälfte
  11      Gehe zurück zu Zeile 3
  12  Sonst
  13      Ende

• Dieser Code hätte wie folgt vereinfacht werden können, um seine rekursiven Eigenschaften hervorzuheben:

  1   Nimm Telefonbuch
  2   Öffne das Telefonbuch in der Mitte
  3   Schau dir die Seite an.
  4   Wenn die Person auf der Seite ist
  5       Rufe die Person an.
  6   Oder wenn die Person weiter vorne steht
  7       Durchsuche die linke Hälfte.
  8   Oder wenn die Person weiter hinten steht
  9       Durchsuche die rechte Hälfte.
  10  Sonst
  11      Ende

• Erinnern Sie sich daran, dass wir in Woche 1 eine Pyramidenstruktur wie folgt erstellen wollten:

    #
    ##
    ###
    ####

  #include <cs50.h>
  #include <stdio.h>
  
  void draw(int n);
  
  int main(void)
  {
      int height = get_int("Height: ");
      draw(height);
  }
  
  void draw(int n)
  {
      for (int i = 0; i < n; i++)
      {
          for (int j = 0; j < i + 1; j++)
          {
              printf("#");
          }
      }
      printf("\n");
  }

• Um dies mit Hilfe von Rekursion zu implementieren, geben Sie code recursion.c in Ihr Terminalfenster ein und schreiben Sie den Code wie folgt:

  #include <cs50.h>
  #include <stdio.h>
  
  void draw(int n);
  
  int main(void)
  {
      draw(1);
  }
  
  void draw(int n)
  {
      draw(n - 1);
  
      for (int i = 0; i < n; i++)
      {
          printf("#");
      }
  
      printf("\n");
  }

  Beachten Sie, dass die Zeichenfunktion sich selbst aufruft. Falls Sie der Compiler nicht davor warnt und Sie diesen Code ausführen, läuft das Programm in einer Endlosschleife. Um diese Schleife abzubrechen, drücken Sie Strg-C auf Ihrer Tastatur. Der Grund dafür, dass eine Endlosschleife entsteht, ist, dass es keine Anweisung gibt, das Programm zu beenden. Es gibt keinen Fall, in dem das Programm fertig ist – der Basisfall wurde nicht implementiert.

• Wir können unseren Code wie folgt korrigieren:

  #include <cs50.h>
  #include <stdio.h>
  
  void draw(int n);
  
  int main(void)
  {
      int height = get_int("Höhe: ");
      draw(height);
  }
  
  void draw(int n)
  {
      // If nothing to draw\
      // (using <= instead of == is super-safe)
      if (n <= 0)
      {
          return;
      }
  
      draw(n - 1);
  
      for (int i = 0; i < n; i++)
      {
          printf("#");
      }
      printf("\n");
  }

  Beachten Sie, dass der Basisfall dafür sorgt, dass der Code nicht ewig läuft: Die Zeile if (n <= 0) beendet die Rekursion. Jedes Mal, wenn draw sich selbst aufruft, ruft es sich selbst mit n-1 auf. Irgendwann wird n-1 gleich 0 sein, was dazu führt, dass die Funktion draw zurückkehrt und das Programm endet.

Merge Sort

• Auf der Suche nach einem effizienteren Sortieralgorithmus können wir nun die Rekursion nutzen und einen sehr effizienten Sortieralgorithmus namens Merge Sort implementieren.

• Der Pseudocode für Merge Sort ist recht kurz:

  Wenn es nur eine Zahl ist
    Ende
  Sonst
    Sortiere linke Hälfte der Zahlen.
    Sortiere rechte Hälfte der Zahlen.
    Führe beide hälften zusammen.

• Betrachten Sie die folgende Liste von 1-stelligen Ziffern:

    6 3 4 1

• Zuerst fragt Merge Sort: “Ist das nur eine Zahl?” Die Antwort ist “Nein”, also fährt der Algorithmus fort.

    6 3 4 1

• Zweitens wird die Sortierfunktion die Zahlen nun in der Mitte teilen (oder so nah wie möglich) und die linke Hälfte der Zahlen sortieren.

    6 3 | 4 1

• Drittens würde sich Merge Sort die Zahlen auf der linken Seite ansehen und fragen: “Ist das nur eine Zahl?” Da die Antwort “Nein” lautet, werden die Zahlen auf der linken Seite in der Mitte geteilt.

    6 | 3

• Viertens wird Merge Sort wieder fragen: “Ist das nur eine Zahl?“ Diesmal lautet die Antwort ja! Daher wird diese Sortiert-Aufgabe beendet und zur letzten Aufgabe, die davor lief, zurückgekehrt:

    6 3 | 4 1

• Fünftens: Mit der Funktion „merge“ werden die Zahlen auf der linken Seite sortiert (wie genau wird im Short-Video zu Merge Sort erklärt).

    3 6 | 4 1

• Nun kehren wir zu dem Punkt zurück, an dem wir im Pseudocode aufgehört haben, nachdem die linke Seite sortiert wurde. Ein ähnlicher Prozess der Schritte 3 bis 5 wird mit den rechten Zahlen durchgeführt. Das Ergebnis wird sein:

    3 6 | 1 4

• Beide Hälften sind nun sortiert. Schließlich fügt der Algorithmus beide Seiten zusammen. Er sieht sich die erste Zahl auf der linken Seite und die erste Zahl auf der rechten Seite an. Er setzt die kleinere Zahl an die erste Stelle, dann die zweitkleinste. Der Algorithmus wiederholt dies für alle Zahlen, was zu folgendem Ergebnis führt:

    1 3 4 6

• Merge Sort ist abgeschlossen, und das Programm wird beendet.

• Merge-Sort ist ein sehr effizienter Sortieralgorithmus mit einer Worst-Case-Laufzeit von $O(n \log n)$. Die Best-Case-Laufzeit ist ebenfalls $O(n \log n)$, da der Algorithmus immer noch alle Werte im Array bearbeiten muss.

• Zum Schluss haben wir uns noch eine Visualisierung angesehen.

  • Weitere Visualisierungen gibt es online.

Zusammenfassend

In dieser Lektion haben Sie etwas über algorithmisches Denken und das Erstellen eigener Datentypen gelernt. Insbesondere haben wir heute folgendes behandelt:

• O-Notation (und $\Omega$).
• Binäre Suche und Lineare Suche.
• Bubble Sort, Selection Sort und Merge Sort.
• Rekursion.

Bis zum nächsten Mal!